For hundreds of years, there was an immutable law of physics that was never challenged: that in any reaction occurring in the Universe, mass was conserved. That no matter what you put in, what reacted, and what came out, the sum of what you began with and the sum of what you ended with would be equal.
But under the laws of special relativity, mass simply couldn’t be the ultimate conserved quantity, since different observers would disagree about what the energy of a system was. Instead, Einstein was able to derive a law that we still use today, governed by one of the simplest but most powerful equations ever to be written down, E = mc2.
There are only three parts to Einstein’s most famous statement:
- E, or energy, which is the entirety of one side of the equation, and represents the total energy of the system.
- m, or mass, which is related to energy by a conversion factor.
- And c2, which is the speed of light squared: the right factor we need to make mass and energy equivalent.

The meaning of this equation is thoroughly world-changing. As Einstein himself put it:
It followed from the special theory of relativity that mass and energy are both but different manifestations of the same thing — a somewhat unfamiliar conception for the average mind.
Here are the three biggest meanings of that simple equation.
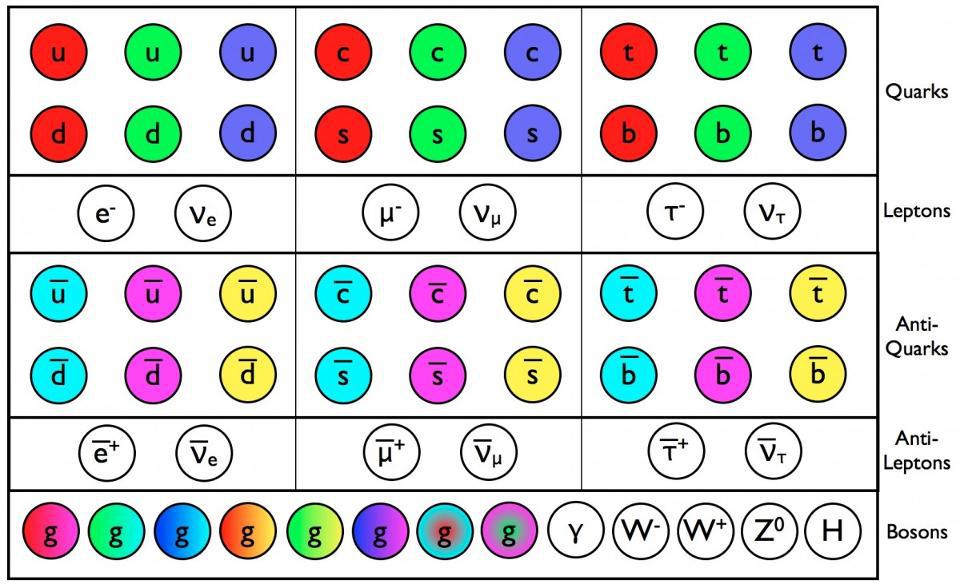
1.) Even masses at rest have an energy inherent to them. You’ve learned about all types of energies, including mechanical energy, chemical energy, electrical energy, as well as kinetic energy. These are all energies inherent to moving or reacting objects, and these forms of energy can be used to do work, such as run an engine, power a light bulb, or grind grain into flour.
But even plain, old, regular mass at rest has energy inherent to it: a tremendous amount of energy. This carries with it a tremendous implication: that gravitation, which works between any two masses in the Universe in Newton’s picture, should also work based off of energy, which is equivalent to mass via E = mc2.
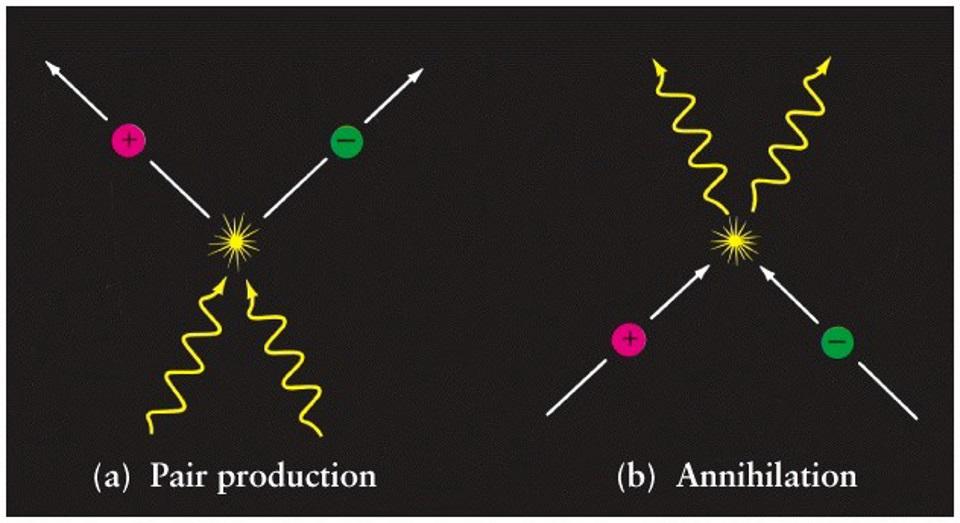
2.) Mass can be converted into pure energy. This is the second meaning of the equation, where E = mc2 tells us exactly how much energy you get from converting mass. For every 1 kilogram of mass you turn into energy, you get 9 × 1016 joules of energy out, which is the equivalent of 21 Megatons of TNT.
When we experience a radioactive decay, or a nuclear fission or fusion reaction, the mass of what we start with is greater than the mass we end up with; the law of conservation of mass is invalid.
But the amount of the difference is how much energy is released! That’s true for everything from decaying uranium to fission bombs to nuclear fusion in the Sun to matter-antimatter annihilation. The amount of mass you destroy becomes energy, and the amount of energy you get is given by E = mc2.

3.) Energy can be used to make mass out of nothing… except pure energy. The final meaning is the most profound. If you take two billiard balls and smash them together, you get two billiard balls out. If you take a photon and and electron and smash them together, you get a photon and an electron out. But if you smash them together with enough energy, you’ll get a photon, and electron, and a new matter-antimatter pair of particles out. In other words, you will have created two new massive particles:
- a matter particle, such as an electron, proton, neutron, etc.,
- and an antimatter particle, such as a positron, antiproton, antineutron, etc.,
whose existence can only arise if you put in enough energy to begin with. This is how particle accelerators, like the LHC at CERN, search for new, unstable, high-energy particles (like the Higgs boson or the top quark) in the first place: by making new particles out of pure energy. The mass you get out comes from the available energy: m = E/c2. It also means that if your particle has a finite lifetime, then due to Heisenberg uncertainty, there’s an inherent unknowability to its mass, since ∆E∆t ~ħ, and therefore there’s a corresponding ∆m from Einstein’s equation, too. When physicists talk about a particle’s width, this inherent mass uncertainty is what they’re talking about.
The fact of mass-energy equivalence also led Einstein to his greatest achievement: General Relativity. Imagine that you’ve got a particle of matter and a particle of antimatter, each with the same rest mass. You can annihilate them, and they’ll produce photons of a specific amount of energy, of the exact amount given by E = mc2.
Now, imagine you had this particle/antiparticle pair moving rapidly, as though they had fallen from outer space, and then annihilated close to the surface of Earth. Those photons would now have extra energy: not just the E from E = mc2, but the additional E from the amount of kinetic energy they gained by falling: from converting gravitational potential energy into the energy-of-motion.
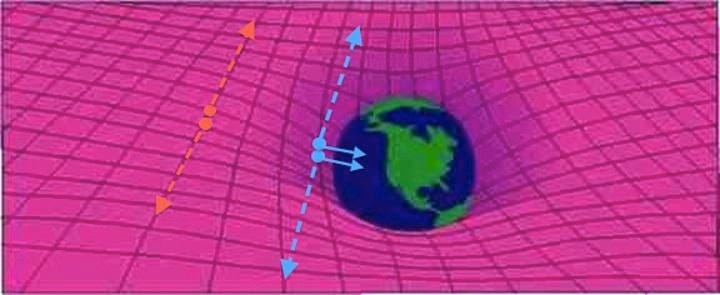
If we want to conserve energy, we have to understand that gravitational redshift (and blueshift) must be real. Newton’s gravity has no way to account for this, but in Einstein’s General Relativity, the curvature of space means that falling into a gravitational field makes you gain energy, and climbing out of a gravitational field makes you lose energy.
The full and general relationship, then, for any moving object, isn’t just E = mc2, but that E2 = m2c4 + p2c2. (Where p is momentum.) Only by generalizing things to include energy, momentum, and gravity can we truly describe the Universe.

Einstein’s greatest equation, E = mc2, is a triumph of the power and simplicity of fundamental physics. Matter has an inherent amount of energy to it, mass can be converted (under the right conditions) to pure energy, and energy can be used to create massive objects that did not exist previously.
Thinking about problems in this way enabled us to discover the fundamental particles that make up our Universe, to invent nuclear power and nuclear weapons, and to discover the theory of gravity that describes how every object in the Universe interacts. And the key to figuring the equation out?
A humble thought experiment, based on one simple notion: that energy and momentum are both conserved. The rest? It’s just an inevitable consequence of the Universe working exactly as it does.
This article was reprinted with permission of Big Think, where it was originally published.