It’s far too early to call “peak ideas”

The following is Chapter 7, Section 2, from the book The Techno-Humanist Manifesto by Jason Crawford, Founder of the Roots of Progress Institute. The entirety of the book will be published on Freethink, one week at a time. For more from Jason, subscribe to his Substack.

In Section 1, we argued that growth is not limited by so-called “natural” resources, which are actually not natural at all, but the product of knowledge.

If ideas, not resources, drive economic growth, then one might well ask: will we run out of ideas?

Some think we already have. The slowdown in GDP and TFP growth since about 1970 is sometimes explained by claiming that all the major opportunities to improve living standards were completed by then, and that no comparable opportunities remain. Robert Gordon’s Rise and Fall of American Growth emphasizes that the innovations of the 1870–1970 period, such as automobiles or electricity, “could only happen once.”¹

But all inventions only happen once: that’s the nature of invention, not a special feature of the period 1870–1970. And there will be things to invent as long as there are problems to be solved—as long as there are any unmet desires, any suffering or death, any frustration or inconvenience; as long as anyone feels cost-conscious about any consumption, from groceries to gasoline to vacations to air conditioning.

Less clear is whether we can keep up the pace of invention. Growth could in theory slow down not because there are no more opportunities to improve the quality of life, but because those improvements get harder to achieve.

We can shed light on this question by turning to economic theory, including quantitative models of economic growth. This will require describing a handful of technical concepts, but the reward is that the best-tested theories of growth will confirm some of the intuitions we’ve already developed, and give us new ones.

By the 20th century, the old land-and-labor model that Malthus had been working with was obsolete. Labor and capital, instead, became the key inputs to economic models. Crucially for economic growth, land is fixed, but capital can be accumulated.

Workers are more productive when given more capital. A farmer with a hoe becomes more productive with a tractor; a factory worker using a hand drill becomes more productive with a power drill. But pure capital accumulation faces diminishing returns. A worker with ten machine tools doesn’t get ten times as productive, since he can only use one at a time. At a certain point, adding more capital per worker isn’t worth the extra expense of depreciation and maintenance. An economy can grow indefinitely by adding both labor and capital, but this does not raise living standards, since what matters for living standards is output per capita.²

To increase output per capita, we need to raise labor productivity, which means we need better capital—that is, more advanced technology. The hand drill becomes a power drill, which becomes a computer-controlled milling machine. The scythe becomes a horse-drawn mechanical reaper, which becomes a gasoline-powered combine harvester.

In the equations of economists, technology is a multiplier on the productivity of labor and capital, called “total factor productivity” or TFP. We can’t measure it directly, but we can deduce its growth by looking at overall economic growth and then taking out the contribution of increased labor and capital. Any growth of output greater than the growth of those inputs is assumed to come from some combination of technology, business organization, and capital allocation.

In the 1950s, economist Robert Solow introduced this parameter and calculated TFP growth for the first time—work that would ultimately win him a Nobel prize.³ He found that from 1909–49, TFP had almost doubled: output per worker had more than doubled, while capital per worker had only increased about 30%. That technology had contributed more to growth than capital was surprising to Solow and his peers; it seemed to “take the capital out of capitalism.”⁴

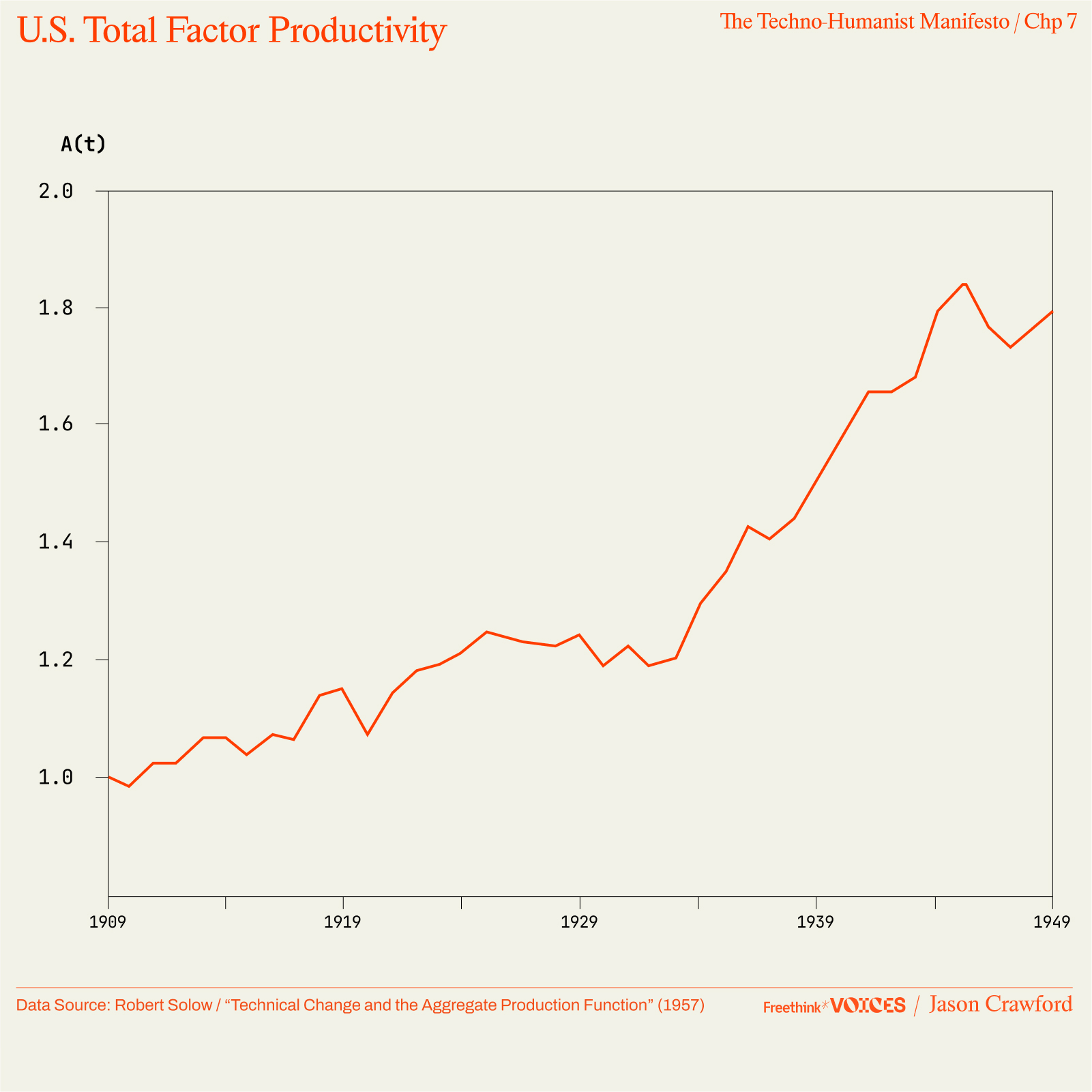
Higher TFP has two effects. First, it multiplies each worker’s productivity. Second, it allows us to afford more capital: when machines create more output, we can afford to spend more on their maintenance and depreciation.⁵ As technology advances and we keep improving and increasing capital, we deploy more capital per worker, and each worker gets more productive. These broad patterns are seen in the economic data over long periods of time, and are well-known to economists as stylized facts that are central to the field.⁶

Holding technology constant, economic output is a linear function of the combined labor and capital inputs. If we double capital and we double labor, we can exactly double production. Two identical factories, staffed with identical workforces, produce twice as much as one factory and one workforce alone.⁷ But if we also double TFP, then we have two better factories equipped with better machines, and we can more than double output. In economics terms, there are “constant returns to scale” from labor and capital alone, but “increasing returns to scale” from labor, capital, and technology together. And increasing returns to scale are what we need to improve living standards.

The lesson from Solow’s economic model is that capital accumulation, alone, cannot sustain progress—but technology can.

Solow measured TFP and observed its growth, but he didn’t explain what drove that growth. Over the coming decades, economists proposed a variety of models. Some had technology provided by the government as a public good.⁸ Others focused on the accumulation of “human capital” (skills and education) rather than technology as such.⁹ Kenneth Arrow proposed a model of “learning by doing”, in which firms improve their techniques as a by-product of production (based on T. P. Wright’s 1936 observation of “experience curves” in airplane manufacturing).¹⁰

What all of these models neglected was private R&D by profit-seeking inventors and firms. But economists who tried to model private R&D faced a dilemma: is technology a public good or a private good? If it was a public good—freely available to all—then there was no incentive for private actors to produce it, and no way for them to recoup their investments in doing so. On the other hand, if it was a private good, it seemed like just another form of capital—in which case it should exhibit constant returns to scale, not increasing returns, when taken together with traditional forms of capital and with labor.¹¹ One paper from the 1960s complained that “the distinction between private and public goods is fuzzy,” and that it depends on legal and social arrangements.¹²

The paradox was resolved in a Nobel-winning 1990 paper by Paul Romer.¹³ He did it by applying two concepts that were, at the time, known within the subfield of public finance, but not broadly applied in other fields:¹⁴ rivalry and excludability. A good is rival if one person’s consumption of it diminishes the amount available to others: normal physical goods such as a loaf of bread are like this, but broadcast radio is not. It is excludable if it is possible to prevent others from consuming it: again, normal physical goods are like this, but unfenced common areas, such as fishing waters, are not. These concepts tease apart two distinct dimensions that are entangled in the one-dimensional classification of “public” vs. “private.” “Private goods” are both rival and excludable. “Public goods” are neither (e.g., national defense). But a good can be one without the other. Romer explains: “Rivalry and its opposite nonrivalry are assertions about production possibilities. Excludability depends on a policy choice about rules.”¹⁵

In particular, ideas, by their nature, are nonrival: they can be replicated at trivial marginal cost and used by everyone simultaneously. Thomas Jefferson remarked that the “peculiar character” of ideas is “that no one possesses the less, because every other possesses the whole of it. He who receives an idea from me, receives instruction himself, without lessening mine; as he who lights his taper at mine, receives light without darkening me.”¹⁶ But ideas can be made at least partially excludable via means such as patents. This allows firms to profit from R&D.

The nonrivalry of ideas, which made previous economists want to think of them as a “public good,” explains how living standards can rise, not fall, with a growing population—how they rise not in spite of but because of a growing population. Romer writes:

But:

There, in a simple formal model, is the refutation of Malthusianism.

No matter what inputs we consider to be driving the economy—land, labor, capital, technology, institutions—scaling just the rival inputs gives us constant returns, but scaling the rival inputs together with nonrival ones gives increasing returns. And again, increasing returns are what is needed to improve living standards.

This model gives the weight of economic theory to our observations about the value of population from Chapter 3. A larger population is better for everyone, because a larger population generates more ideas, and everyone can benefit from them without diminishment. “That ideas should freely spread from one to another over the globe,” wrote Jefferson, “for the moral and mutual instruction of man, and improvement of his condition, seems to have been peculiarly and benevolently designed by nature, when she made them, like fire, expansible over all space, without lessening their density in any point.”¹⁸

So the growth of knowledge, represented by TFP, is crucial to progress. It enables higher living standards, it overcomes resource scarcity, it frees us from the Malthusian trap. The most crucial question for the future of growth, then, is: what drives TFP?

Looking back at the pattern of accelerating growth we saw in the previous chapter, Romer suggested that the growth rate was proportional to the investment in R&D.¹⁹ On the face of it, this is a reasonable hypothesis. But soon after, Chad Jones pointed out that, contrary to the very long-term pattern of increasing growth rates, growth has actually held quite steady for more than 100 years—despite massive increases in the number of researchers and total R&D investment.²⁰ More recently, a paper by Bloom, Jones, van Reenan, and Webb found that this pattern holds not only at the macro level but in various specific industries.²¹

Consider one of the prime examples of sustained exponential progress: Moore’s Law. What investment is required to maintain exponential growth in the number of transistors in an integrated circuit? Bloom et al. define a metric of investment which is the amount spent on R&D by the semiconductor industry, deflated by the wage rate of high-skilled workers (who are the ones doing R&D). They find that in 2014, it took 18 times as much investment by this metric to drive Moore’s Law than it did in 1971.

Why? In the early days of IC manufacturing, when feature sizes were 10 microns, the challenges were things like mechanizing manual processes, or using more sophisticated optical systems to obviate the need for the lithography mask to come into physical contact with the chip.²² Now that features are measured in nanometers, lithography has to be performed with extreme ultraviolet light, feature etching is marred by the nanoscale randomness of individual atoms and photons, electrons threaten to quantum-tunnel right through our logic gates, and the chips generate so much heat you could cook dinner on them.²³ The further we push technology, the harder the problems become to solve.

We see the same pattern in other areas of technology. In the 1700s, labor productivity in textile manufacturing could be improved by multiples via very simple devices such as the flying shuttle or the cotton gin. Today, the fiber-to-fabric pipeline is already so highly automated that to get a similar multiplier would be a much bigger challenge.²⁴

We see the same pattern again in science. Galileo became a legendary scientist by rolling balls down inclined planes and observing the planets through simple, low-powered telescopes. Now, to push forward the frontiers of science, we build such massive, expensive instruments as the James Webb Space Telescope, the Large Hadron Collider, and the Laser Interferometer Gravitational-wave Observatory (LIGO)—collaborations between thousands of researchers that require hundreds of millions or even billions of dollars of investment.²⁵

We might think of ideas like apples in an orchard, which become harder to reach as we pick off the low-hanging fruit. Jones calls the effect “fishing out,” as if ideas were a finite number of fish stocked in a closed pond, such that as we empty the pond of fish, it becomes harder to catch them.²⁶ Others have used the metaphor of mining for ideas, where any vein of ideas can run thin.²⁷

Jones’s fishing-out effect is the flip side of Romer’s increasing returns. Both are consequences of the non-rivalry of ideas. The upside of this non-rivalry is that when an idea is created, everyone can share it. But the downside is that we can’t generate more value by generating the same idea over again year after year, nor can two people or teams generate twice the value by each generating the same idea.²⁸

On top of this, we can add the “burden of knowledge.” The more we learn, the longer a researcher has to study in order to reach the frontier, where they can make progress; and the more they have to specialize, which makes it harder to forge connections across disparate fields.²⁹

If we imagine the frontier of knowledge and technology as an expanding sphere, we might suppose that each researcher or lab can only push forward a constant surface area—thus as the sphere expands, we need more researchers to join the effort all the time in order to keep pushing the whole thing outwards. Altogether, as we advance the frontier, we face a greater quantity and quality of problems to be solved—more problems because of the specialization of fields, and harder problems because the low-hanging fruit gets picked.

Bloom et al. provocatively titled their paper “Are Ideas Getting Harder to Find?” And in Jones’s formal models, this is represented by TFP itself having diminishing returns on future TFP growth.³⁰ Some have interpreted this as a prediction of stagnation in the future—decreasing growth rates and slowing progress, as ideas continue to get harder to find—or even as an explanation for the slowdown in recent decades.³¹

But Jones’s model does not predict stagnation. Fishing-out is only one factor affecting growth rates. Remember, ideas have been getting harder to find ever since the Stone Age! There was so much low-hanging fruit in the Stone Age. If this were the only factor, then the long-term pattern of history would be one of deceleration, not acceleration.

The other side of the equation is that as ideas get harder to find, we get better at finding them. As the quantity and quality of the problems we have to solve increases, so does the quantity and quality of the resources we bring to bear on that challenge—more and better-educated researchers, working with more and better-designed tools.

The lesson of these models is not that stagnation is inevitable. They were originally developed to explain constant growth, not slowing growth. The lesson, instead, is about the intensity of inputs required to sustain growth. A constant base of R&D can’t sustain exponential growth. Exponential growth in R&D inputs is required for exponential growth in the economy. And super-exponential growth in those inputs can generate super-exponential economic growth. This is in fact what has happened over the long run of human history—the accelerating pattern we saw in the last chapter.³²

Note that all the metaphors people use for innovation—fruit-picking, fishing, mining—are analogies to physical resource extraction. The comparison is instructive, given what we have discussed above about resources. Ideas get harder to find, but resources do too, and in both cases our investment in discovery and exploitation ramps up to meet the challenge: just as we continue to extract copper from lower-grade ores, we can continue to solve more difficult problems in science and technology. A particular field of ideas can run out, like an oil field or a mine—but just as we find new deposits of minerals, we also find new fields of innovation that open up the possibility for rapid advancement, such as computing in the 20th century or mRNA technology in the 21st. So just as it’s always been a mistake to call Peak Resources, I think it’s far too early to call Peak Ideas.

---

If there is truly a vast unexplored space of productive ideas remaining, and all we need to find them is a sufficient number of intelligent people, then our final concern for long-term growth might be: will we run out of people?

As noted in the last chapter, accelerating growth is driven by several self-reinforcing factors, including the base of ideas in science and technology, the industrial infrastructure we have built out, the surplus wealth we have to invest in R&D, and the total population, which gives us more brains to create more ideas.

All of these factors are growing, and we can expect them to continue to grow—except people. Population growth has fallen dramatically in recent decades and shows no signs of bottoming out. We have already passed “peak child.”³³ UN projections show population growth reaching zero by the end of the century, with population leveling out at maybe eleven billion.³⁴

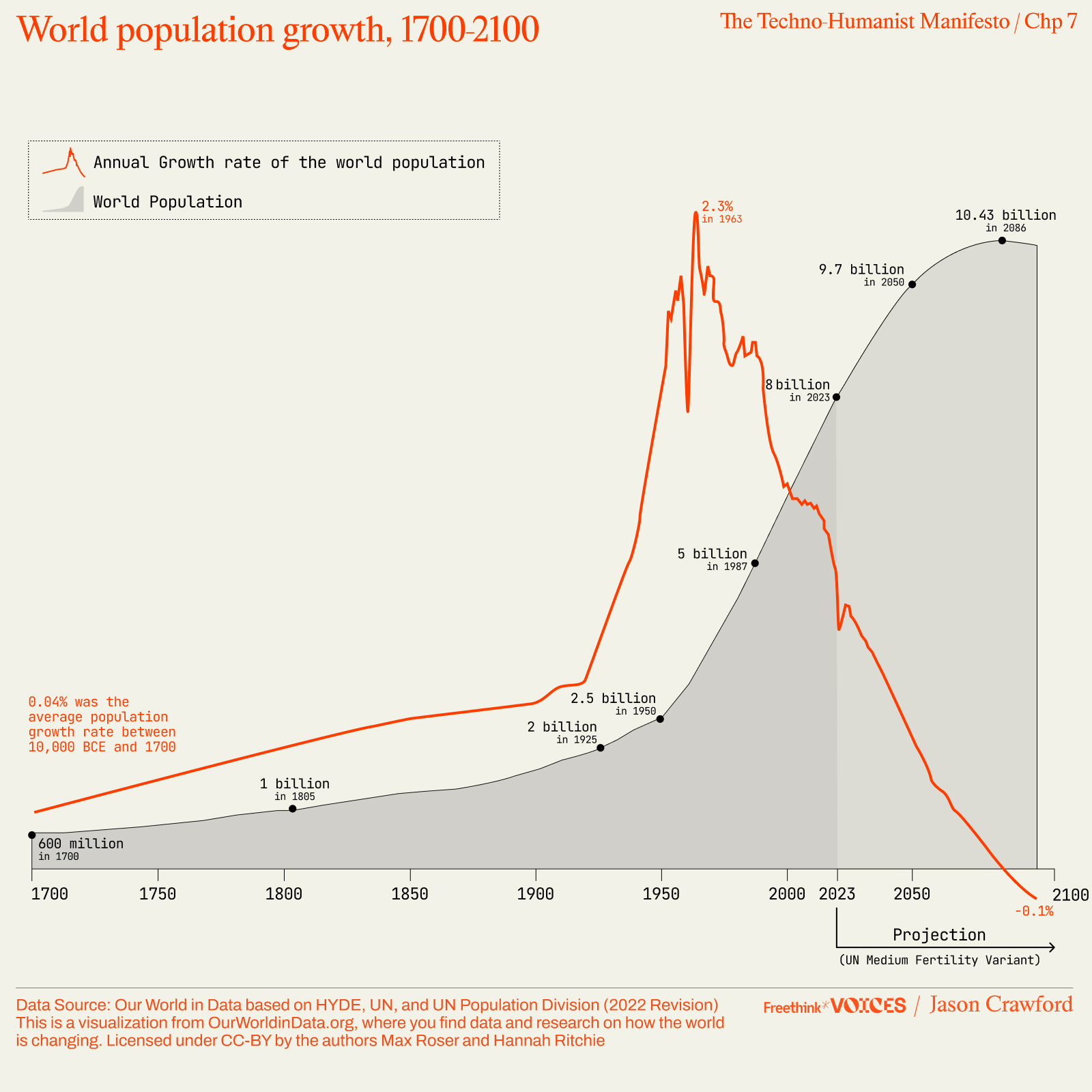
There is no consensus among economists about which factors are crucial and how they quantitatively interact. But in Jones’s model, labor—that is, the number of researchers—is the driving factor. Under this model, if population were to level off as per UN estimates, economic growth would asymptote to zero, as we picked off all the low-hanging fruit. The frontier would get harder and harder to push out, and with only a constant base of researchers, progress would get slower and slower. No more acceleration, not even exponential growth, just a gentle plateau.³⁵

There are a few ways we could stave off this stagnation. For one, the number of researchers is still only a fraction of a percent of the population. More people could become researchers, especially in large countries that are rising in affluence and education, such as India and China.³⁶ This might take us a long way, but eventually it will level out, as the research fraction of the population can never exceed 100%.

A somewhat longer-term solution would be to reverse the decline in population growth—without, of course, regressing to a world in which couples had little ability to control fertility and women had little choice about what to do with their lives anyway. It might instead reverse through a combination of cultural, political, economic, and technological factors. Policy reform could reduce the cost and burden of caring for children, by relaxing regulation on everything from car seats to daycare.³⁷ The general increase of wealth might allow families to afford more children while still maintaining the lifestyle they desire; governments may decide to help at the margin through increased subsidies.³⁸ Advanced biotech may make it easier to prolong fertility later into life, or to reduce the burden of childbearing.³⁹ AI companions might keep children entertained in a form that is healthy and educational, relieving parents of the guilt of “screen time.” Social movements could help steer parents away from burdensome “helicopter parenting” and into a more relaxed, “free range” parenting style; or help to remind prospective parents of the joy of young children and the value of having grown children in one’s old age.⁴⁰ A shift in the zeitgeist could raise the honor and prestige of parenting, or quell the pessimism about the future that makes some people wary of bringing children into the world (especially if those children are perceived primarily as a carbon footprint).⁴¹ Likely none of these is a silver bullet for the fertility decline—which is widespread across cultures and is notoriously difficult to affect with policy—but a combination of all of them might slowly turn the trend around. Even if successful, however, this will hit social and biological limits—enough to keep up exponential growth, but not accelerating growth.

Beyond continuously increasing the number of researchers, another possibility is continuously increasing researcher productivity, through more and better tools. Surely scientists and engineers have been able to do more as we went from making calculations with pen and paper, to using a slide rule, to a mechanical calculator, to a computer. But of course, progress in such tools has been happening for a long time, so it is already contributing to growth and acceleration, and there’s no reason to think that we can increase this factor faster to make up for any shortfall in researchers. Also, remember the challenge of diminishing returns: there is only so much capital that can profitably be deployed per worker, and this must hold in the production of ideas as much as in the production of goods.⁴²

Unless we can automate the production of ideas completely. If, as some have predicted, AI researchers can advance science and technology on their own, then humans are no longer the bottleneck on progress.

Silicon researchers could overcome biological limitations. They could overcome the burden of knowledge: they would be instantiated with training and skills, rather than requiring a lengthy education; and they could have encyclopedic recall of the scientific literature. They could also overcome the fishing-out effect, by sheer scale: they would work faster and cheaper than human researchers, and they would be faster and cheaper to create, with no biological limitations—only sufficient capital for GPUs and the energy to run them. In short, they could be the solution to driving the next era of growth and progress.

Regardless of how this plays out, notice that in the course of this chapter we’ve gone from worries about overpopulation to worries about underpopulation. That signifies the shift from a view of humans as primarily consumers and wasters to one of them as producers and idea-generators.

To be continued in Chapter 7, Section 3.

Parts of this essay were adapted from “Ideas getting harder to find does not imply stagnation.”

---

1: Gordon, Rise and Fall of American Growth, 641.

2: Tabarrok, “Introduction to the Solow Model.”

3: Solow, “A Contribution to the Theory of Economic Growth” (1956) and “Technical Change and the Aggregate Production Function” (1957).

4: Gordon, Rise and Fall of American Growth, 569.

5: Tabarrok, “Introduction to the Solow Model.”

6: Kaldor, “Capital Accumulation and Economic Growth.” Jones and Romer, “The New Kaldor Facts.”

7: This intuition pump is known as the “standard replication argument.” See Jones, “Paul Romer: Ideas, Nonrivalry, and Endogenous Growth.”

8: Shell, “Toward a Theory of Inventive Activity and Capital Accumulation.”

9: Uzawa, “Optimum Technical Change in An Aggregative Model of Economic Growth”; Lucas, “On the Mechanics of Economic Development.”

10: Arrow, “The Economic Implications of Learning by Doing”; Wright, “Factors Affecting the Cost of Airplanes.”

11: I am oversimplifying the problem somewhat; other papers ran into more subtle, technical issues. For instance, in some learning-by-doing models, advantages can accrue to the largest companies in a way such that each industry tends towards monopoly: Dasgupta and Stiglitz, “Learning-by-doing, Market Structure and Industrial Trade Policies.”

12: Shell, “Toward a Theory of Inventive Activity and Capital Accumulation.”

13: Romer, “Endogenous Technological Change.” ​​

14: Romer, “Nonrival Goods After 25 Years.”

15: Ibid.

16: “Thomas Jefferson to Isaac McPherson, 13 August 1813.” I have modernized spelling and capitalization.

17: Romer, “Speeding Up: Theory.”

18: “Thomas Jefferson to Isaac McPherson, 13 August 1813.”

19: Romer, “Endogenous Technological Change.” ​​

20: Jones, “R\&D-Based Models of Economic Growth”; “Time Series Tests of Endogenous Growth Models.”

21: Bloom et al., “Are Ideas Getting Harder to Find?”

22: Burbank, “The Near Impossibility of Making a Microchip.”

23: Duque, “Pushing the Boundaries of Moore’s Law,” Može et al., “Experimental and Numeric Heat Transfer Analysis,” Sperling, “Quantum Effect at 7/5nm and Beyond.”

24: “Flying Shuttle”; “Paving the way toward the smart spinning mill.”

25: “James Webb Space Telescope,” “US Scientists Celebrate the Restart of the Large Hadron Collider,” “The LIGO Scientific Collaboration,” “U.S. Completes $531M Contribution to Large Hadron Collider Project,” Jones, “ LIGO: Looking Ahead, Looking Back.”

26: Jones, Growth and Ideas, 1071.

27: Karnofsky, “Where’s Today’s Beethoven?”

28: For a formal model of research as a random search process, where new inventions are valuable and patentable only if they are better than the state of the art, see Kortum, “Research, Patenting, and Technological Change.”

29: Clancy, “Are Ideas Getting Harder to Find?”

30: Jones, “R\&D Models of Economic Growth.”

31: Southwood, “Scientific Slowdown is not Inevitable.”

32: For a model of long-run economic history that replicates the pattern of acceleration, see Jones, “Was an Industrial Revolution Inevitable?”

33: Ritchie, “The World Has Passed Peak Child.”

34: Roser and Ritchie, “Two Centuries of Rapid Population Growth Will Come to an End.”

35: Jones, “The End of Economic Growth?”

36: Jones, “The Past and Future of Economic Growth.”

37: Nickerson and Solomon, “Car Seats as Contraception”; Flowers et al., “Childcare Regulation and the Fertility Gap.”

38: Tabarrok, “The 2nd Demographic Transition,” Myrskylä et al., “Advances in Development Reverse Fertility Decline.”

39: Constantin, “Artificial Wombs When?”

40: Caplan Selfish Reasons To Have More Kids; also Lenore Skenazy, Free-Range Kids.

41: Carrington, “Climate ‘apocalypse’ fears stopping people having children”; Blum, “How Climate Anxiety Is Shaping Family Planning.” These and additional examples found in Scott Alexander, “Please Don’t Give Up On Having Kids Because of Climate Change.”

42: Jones, “The Past and Future of Economic Growth.”